Молчанов И.Н., Герасимова И.А.

 

 

КОМПЬЮТЕРНЫЙ ПРАКТИКУМ ПО НАЧАЛЬНОМУ КУРСУ ЭКОНОМЕТРИКИ (РЕАЛИЗАЦИЯ НА EVIEWS)

Практикум

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Ростов-на-Дону

2001

УДК [330.43](076.5)

М 75

1Л4

Молчанов И.Н., Герасимова И.А. Компьютерный практикум по начальному курсу эконометрики (реализация на Eviews): Практикум /Ростовский государственный экономический университет. - Ростов-н/Д., - 2001. – 58 с. - ISBN 5-7972-0377-4.

 

Практикум представляет собой попытку создания учебного пособия, ориентированного на специфику преподавания эконометрики в экономическом вузе с использованием специализированного эконометрического пакета Eviews. Практикум ориентирован на начальный курс эконометрики.

Для студентов и аспирантов вузов, обучающихся по экономическим специальностям.

 

 

Замечания и предложения просим направлять по адресу:

344007, г.Ростов-на-Дону, ул. Большая Садовая, 69, к. 404, каф. СМиП.

 

 

 

Рецензенты:

Л.И.Ниворожкина, доктор экономических наук, профессор, зав. кафедрой СМиП РГЭУ «РИНХ».

В.С.Князевский, доктор экономических наук, профессор, Заслуженный деятель науки Российской Федерации, РГЭУ «РИНХ».

 

 

Утверждено в качестве практикума редакционно-издательским советом РГЭУ

 

 

ISBN 5-7972-0377-4

 

	Ó Ростовский государственный экономический университет «РИНХ», 2001
	Ó Молчанов И.Н., Герасимова И.А., 2001

Предисловие

Эконометрический пакет Eviews обеспечивает особо сложный и тонкий инструментарий обработки данных, позволяет выполнять регрессионный анализ, строить прогнозы в Windows-ориентированной компьютерной среде. С помощью этого программного средства можно очень быстро выявить наличие статистической зависимости в анализируемых данных и затем, используя полученные взаимосвязи, сделать прогноз изучаемых показателей.

Целесообразно выделить следующие сферы применения Eviews:

Ø     анализ научной информации и оценивание;

Ø     финансовый анализ;

Ø     макроэкономическое прогнозирование;

Ø     моделирование;

Ø     прогнозирование состояния рынков.

Особо широкие возможности открывает Eviews при анализе данных, представленных в виде временных рядов.

Подробную информацию об условиях приобретения и распространения пакета можно получить на сайте производителя: http://www.eviews.com . Пакет занимает после инсталляции около 12 Мб на жестком диске.

Все используемые в практикуме задания (примеры) доступны в виде файлов в формате Excel и Eviews по адресу: http://molchanov.narod.ru/econometrics.html .

При выполнении предлагаемых заданий могут оказаться полезными следующие учебники и пособия:

1.     Айвазян С.А., Мхитарян В.С. Прикладная статистика и основы эконометрики. – М.: ЮНИТИ, 1998. – 1022 с. ISBN 5-238-00013-8.

2.     Доугерти К. Введение в эконометрику. - М.: ИНФРА-М, 1997. – XIV, 402 с.: ил. - (Университетский учебник) Библиография: с.384-386. ISBN 5-86225-458-7; 0-19-50346-4.

3.     Елисеева И.И. Эконометрика: Учебник /И.И.Елисеева и др. – М.: Финансы и статистика, 2001. – ISBN 5-279-01955-0.

4.     Князевский В.С., Житников И.В. Анализ временных рядов и прогнозирование: Учеб. пособие. – Ростов-на-Дону: РГЭА, 1998. – 161 с.

5.     Князевский В.С., Молчанов И.Н. Статистические расчеты на компьютере с использованием ППП Microstat. - Ростов-на-Дону: РГЭА, 1996. - 86 с.

6.     Магнус Я.Р., Катышев П.К., Пересецкий А.А. Эконометрика. Начальный курс. – М.: Дело, 2000. – 400 с. ISBN 5-7749-0055-X.

7.     Практикум по эконометрике: Учеб. пособие /И.И.Елисеева и др. – М.: Финансы и статистика, 2001. – 192 с. ISBN 5-279-02313-2.

8.     Greene, W.H. Econometric analysis, Prentice Hall, 4^th Edition, 2000. – 1004 p.

9.     Verbeek, M. A Guide to Modern Econometrics, Wiley, 2000. – 400 p.

Практическое занятие № 1.

«Знакомство с эконометрическим пакетом Eviews»

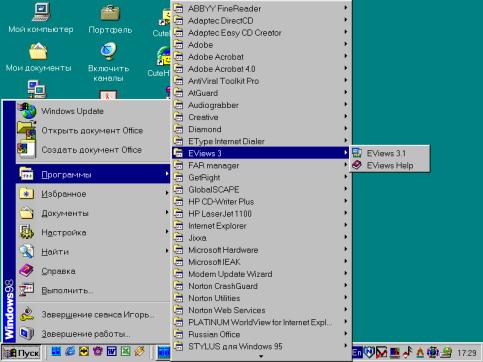
Eviews (далее пакет) установлен в директорий Program Files/Eviews3. Запуск осуществляется выбором соответствующего значка в панели Пуск/Программы/Eviews3/Eviews 3.1 (файл C:\Program Files\EViews3\EViews3.exe) (см. рис. 1) или щелчком (двойным щелчком – в зависимости от установок) по соответствующей пиктограмме на рабочем столе.

Рис. 1.

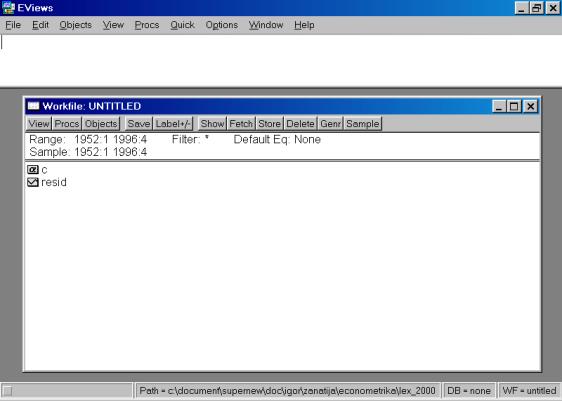
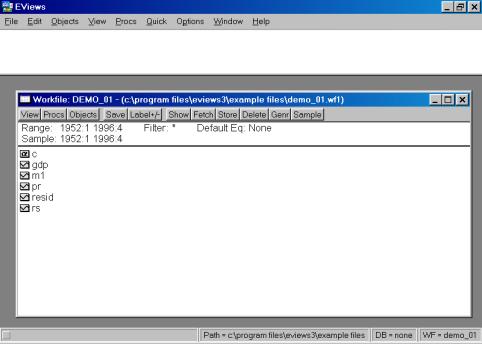
Если Вы все сделали правильно, появится стартовое окно пакета (рис.2).

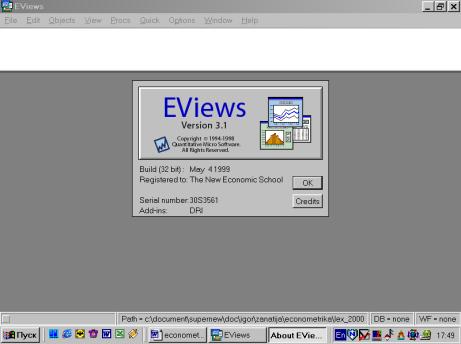
Рис. 2.

Если в настоящий момент окно, содержащее пакет, является активным, то первая строка экрана (Title Bar) будет темнее остальных. При переключении в другое окно цветовая окраска данной строки изменит цвет на более приглушенный (серый).

Ниже следует строка основного меню (Main Menu). Принцип его построения прост – при нажатии на соответствующие клавиши появляется раскрывающееся меню (drop-down menu). Доступные в настоящий момент опции являются затемненными (darkened menu items). Те пункты, с которыми в настоящий момент работа невозможна, приглушены (grayed menu items).

Далее располагается командная строка (окно) (command window). В нем происходит непосредственный набор команд, которые выполняются после нажатия клавиши Enter (Ввод). Для исполнения многих команд отсутствует необходимость их набора – просто надо выбрать нужный пункт в основном меню.

Большая часть экрана пакета отведена под рабочую область (work area). В ней размещаются рабочие объекты. Переключение между ними осуществляется нажатием клавиши F6.

Последняя область экрана показывает текущее состояние (status line) пакета (рабочий каталог, текущий файл и др.).

Завершение работы с пакетом осуществляется путем выбора в командной строке опции File/Exit. Система предложит сохранить/не сохранить имеющиеся данные. Если имя файла не было задано ранее, автоматически будет предложено имя UNTITLED. Его можно изменить на любое другое. Пакет имеет обширную справочную систему (пункт основного меню Help).

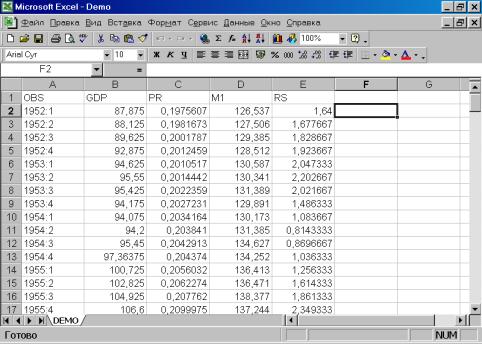
Знакомство с пакетом начнем с файла, содержащего данные о совокупном спросе на деньги (M1) – (aggregate money demand) (M1) – зависимая переменная; независимые: доход (ВВП) - income (GDP); уровень цен (PR) - price level (PR); краткосрочная процентная ставка (RS) - short term interest rate (RS).

Проведем некоторые преобразования и расчеты.

Первым шагом создадим новый рабочий файл (workfile). Его имя должно иметь следующий вид и состоять только из латинских букв: Номер_группы_demo_01.wf1 (расширение wf1 присваивается автоматически). Например: 451_demo_01.wf1. Расположить его следует в директории, относящемся к Вашему факультету (внимательно ознакомьтесь с памяткой в компьютерном классе). Исходные данные находятся в файле Excel. Они должны быть импортированы в пакет. Создание рабочего файла начнем с того, что выберем File/New/Workfile в основном меню (см. рис. 3).

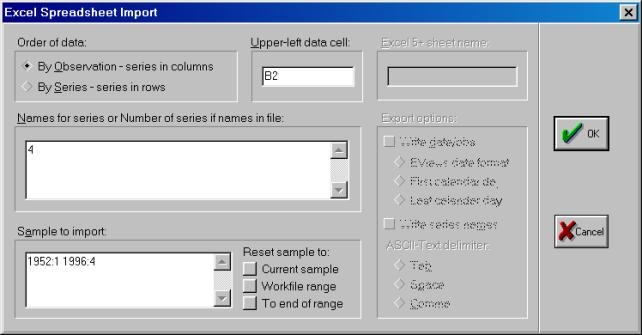
После нажатия на кнопке со словом Workfile откроется диалоговое окно, с помощь которого можно задать тип вводимых Вами данных (см. рис. 4).

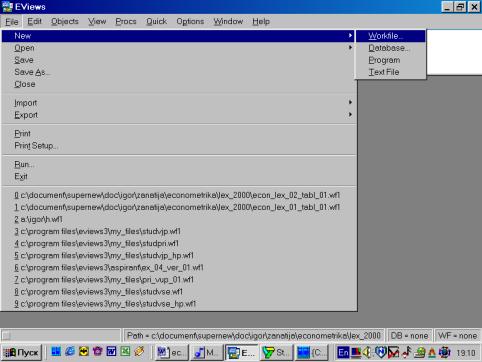
Рис. 3.

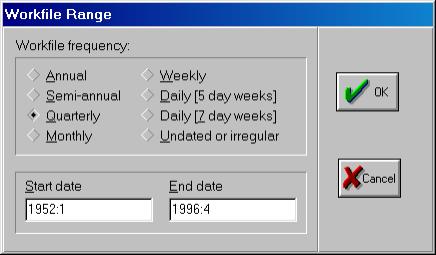
Рис. 4.

Как видно из рис. 4, в пакете допускается  восемь типов данных. Это могут быть:

·       Годовые (Annual) – годы 20 в. идентифицируются по последним двум цифрам (97 эквивалентно 1997), для данных, относящихся к 21 в. необходима полная идентификация (например, 2020);

·       Полугодовые (Semi-annual) – 1999:1, 2001:2 (формат – год и номер полугодия);

·       Квартальные (Quarterly) – 1992:1, 65:4, 2005:3 (формат – год и номер квартала);

·       Ежемесячные (Monthly) – 1956:1, 1990:11 (формат – год и номер месяца);

·       Недельные (Weekly)  и дневные (5/7 day weeks) – допускаются форматы Месяц/День/Год (по умолчанию) и (День/Месяц/Год) – настроить эту опцию можно в меню Options/Frequency Conversion & Date Display. Так, введенные числа 8:10:97 будут интерпретированы как Август, 10, 1997. Для установки, принятой в Европе, начальная дата будет выглядеть как Октябрь, 8, 1997;

·       Недатированные или нерегулярные (Undated or irregular) – допускают работу с данными, строго не привязанными к определенным временным периодам.

Важным является указание начальной (start) и конечной (end) даты/наблюдения (date/observation).

В нашем примере начальным периодом является первый квартал 1952 г. (1952:1), конечным – четвертый квартал 1996 г. (1996:4).

Закончив ввод временных периодов, надо нажать клавишу OK. Пакет создаст рабочий файл без имени, и на дисплее в рабочей области появится окно (см. рис. 5). Все рабочие файлы пакета всегда содержат вектор коэффициентов C и серию RESID.

Рис. 5.

Следующим шагом является просмотр исходных данных, содержащихся в исходном файле по адресу Program Files/Eviews3/Example files/demo.xls (формат Exсel версии 5.0 и младше). Важное замечание: имеющаяся версия пакета позволяет импортировать файлы Excel не старше версии 5.0. В противном случае будет выдано сообщение об ошибке. Всегда сохраняйте свои файлы как файлы Microsoft Excel 5.0/95. Для визуализации данных необходимо запустить табличный процессор Excel (действия аналогичны запуску Eviews). Результат представлен на рис. 6. Ознакомившись с данными, файл, подлежащий экспортированию, необходимо закрыть.

Рис. 6.

Для чтения данных, созданных в других программах, надо выбрать в рабочем файле опцию Procs/Import/Read Text-Lotus-Excel… (см. рис. 7). Появится диалог, представленный на рис. 8.

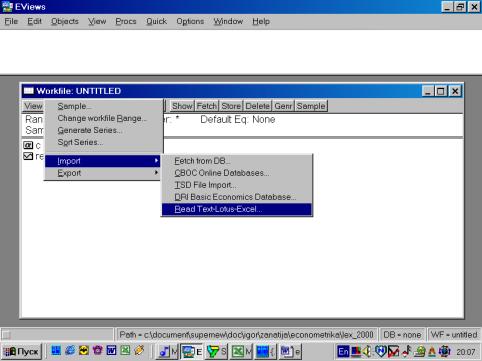
Рис. 7.

Перейдем к папке, содержащей искомый файл (для упрощения поиска в опции Тип файлов (Files of type) можно выбрать Excel.xls (см. рис.8). Для того, чтобы пакет «помнил» Ваши перемещения по папкам компьютера, можно поставить флажок в опции Update default directory (см. рис. 8).

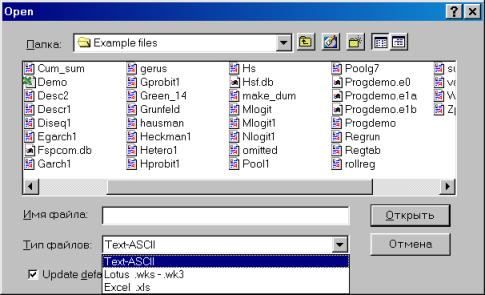
Рис. 8.

Наведем курсор на файл demo.xls и нажмем кнопку Открыть (см. рис. 8). Появится диалог открытия электронных таблиц формата Excel (см. рис. 9).

Рис. 9.

По умолчанию в окне, представленном на рис. 9, предполагается, что данные находятся в столбцах (by observation - series in columns). Если данные представлены в виде серий в строках, то надо отметить другую опцию (By series - series in rows).

Окно Upper-left data cell (левая верхняя ячейка данных) автоматически отобразило клетку B2. Это означает, что данные будут импортироваться из исходной таблицы с клетки, указанной в этом окне (тем самым первая строка и первый столбец будут пропущены). Это вполне соответствует структуре нашего исходного файла (см. рис. 6). Иногда приходится исправлять адрес такой клетки на актуальный.

В окне Names for series or Number of series if names in file (имена для серий или число серий, если имена содержатся в файле) указываем цифру 4. Это связано с тем, что исходный файл (см. рис.6) содержит 4 переменные, находящиеся в столбцах. Имена для этих переменных будут взяты из первой строки электронной таблицы (клетки B1:E1). В том случае, когда необходимо импортировать часть данных (например, только первые две переменные), надо ввести их количество (цифра 2). Если имена переменных, по каким либо причинам, в исходном файле не заданы, можно вместо цифр ввести их имена (латинскими буквами). Если количество переменных, введенных в рассматриваемом окне, превышает количество реально существующих, то в рабочий файл будет введен столбец с заданным именем без данных (обозначаются такие клетки как NA). Если все другие установки удовлетворяют заданным Вами условиям, то можно нажать кнопку OK. Появится окно, отображенное на рис. 10.

Рис. 10.

После того, как исходные данные перенесены Вами в рабочую область пакета (появились имена переменных), надо провести их верификацию (проверку правильности). Вам необходимо создать новую группу, содержащую все импортированные серии (переменные). Это делается следующим образом: необходимо кликнуть мышкой по имени первой переменной (например, GNP), затем, удерживая клавишу  CTRL кликнуть по переменным M1, PR и RS. Все серии на экране будут зачернены. Затем необходимо подвести курсор мыши на зачерненную область экрана и кликнуть правой кнопкой. Далее необходимо выбрать опцию Open. Пакет откроет диалоговое окно со следующими опциями (см. рис. 11).

Выберем Open Group (открыть в одной группе). Пакет создаст группу с именем UNTITLED, в которую войдут все переменные (серии). По умолчанию, данные будут представлены в виде электронной таблицы (возможны другие варианты представления) – см. рис. 12.

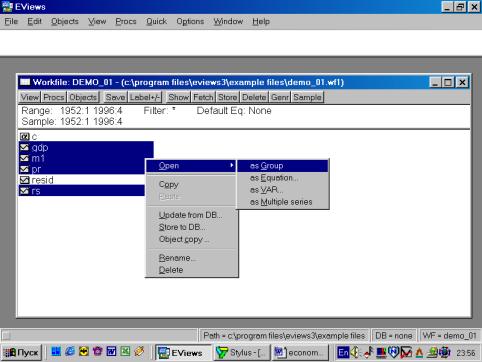
Рис. 11.

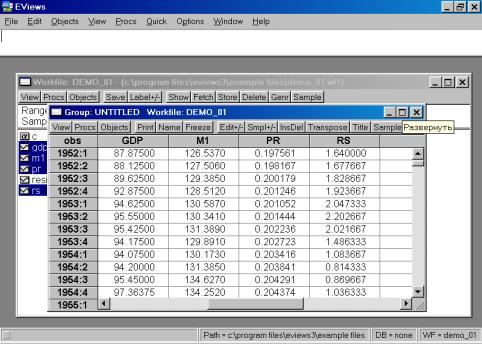
Рис. 12.

Проведите визуальную проверку корректности данных. Сравните, как разместились переменные из исходного файла, обратите внимание на столбец слева от первой переменной (он серого цвета). В нем отображены годы и порядковые номера кварталов. Полученной новой группе данных можно дать имя. Для этого необходимо нажать кнопку Name в текущем окне (см. рис. 12). Появится диалоговое окно (рис. 13.). Автоматически будет предложено имя – GROUP01. Его можно принять, нажав кнопку OK. В рабочем файле сразу добавится одна переменная с введенным Вами именем. Теперь к ней всегда можно перейти простым нажатием клавиши мыши.

Рис. 13.

Образованную Вами группу можно просматривать не только в виде электронной таблицы. Если, находясь внутри GROUP01, выбрать последовательность команд View/Multiple Graphs/Line (см. рис. 14), то данные предстанут не в виде таблицы, а как линейные графики по каждой серии (переменной) – см. рис. 15.

Рис. 14.

Для того, чтобы вернуться к прежней форме представления данных (например, электронной таблице), надо выбрать View/Spreadsheet.

Для просмотра числовых характеристик (описательных статистик) отмеченных переменных необходимо выбрать в рабочем файле View/Descriptive Stats/Individual Samples (см. рис. 16).

В результате появится окно, представленное на рис. 17. В нем содержатся:

Mean – Среднее арифметическое значение;

Median – Медиана;

Maximum – Максимальное значение;

Minimum – Минимальное значение;

Std. Dev. – Стандартное отклонение (среднее квадратическое отклонение);

Skewness – Коэффициент асимметрии;

Kurtosis – Эксцесс;

Probability – Вероятность;

Observations – Количество наблюдений.

Рис. 15.

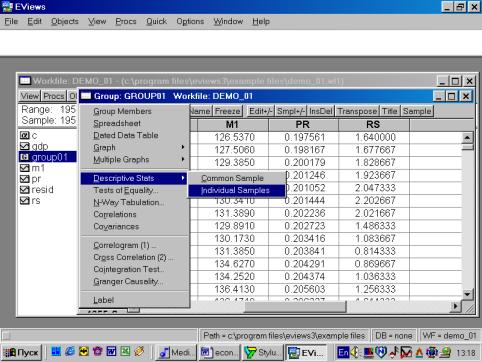
Рис. 16.

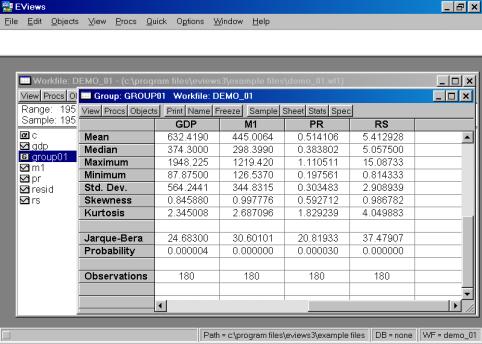
Рис. 17.

Если возникает необходимость проанализировать матрицу коэффициентов корреляции, то необходимо выбрать View/Correlations. Результат представлен на рис. 18.

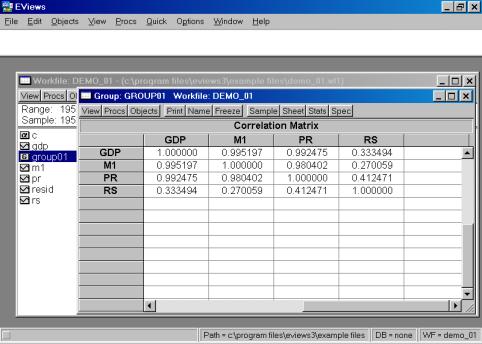
Рис. 18.

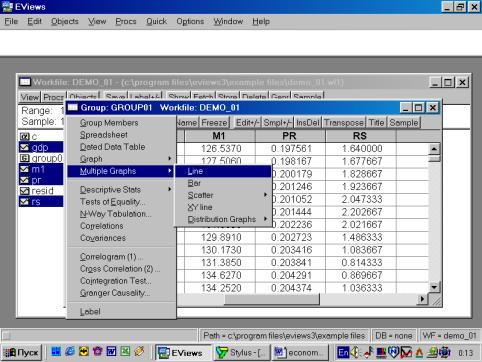
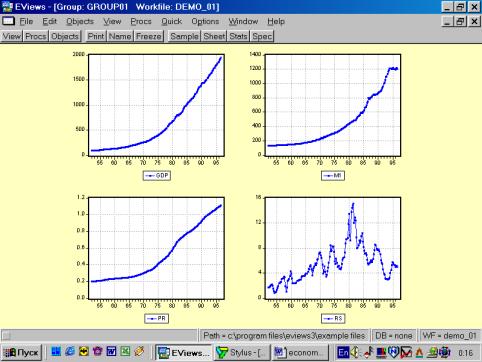
Вы также можете исследовать характеристики для отдельных серий (переменных), совместив вывод диаграммы и числовых характеристик. Дважды кликните на имени серии (например, на переменной М1)  и выберете в рабочем файле пункт меню View/Descriptive Stats/Histogram and Stats (см. рис. 19). Результат наглядно виден на рис. 20.

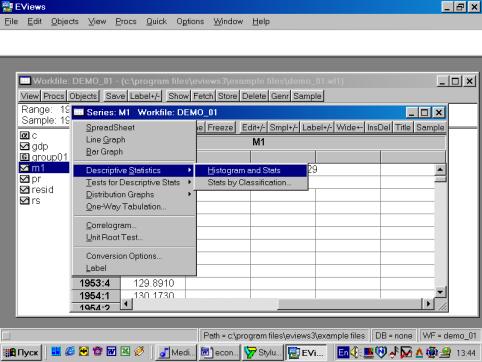
Рис. 19.

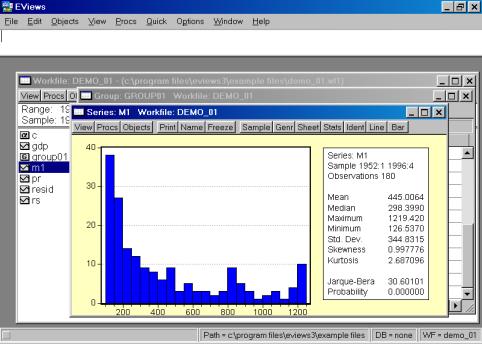
Рис. 20.

С другими возможностями пакета Вы познакомитесь на последующих занятиях.

Для индивидуальной работы по предложенной выше схеме предназначены нижеследующие данные. Подумайте, все ли данные необходимо заносить в электронную таблицу или импортировать из неё.

Пример 1. Стоимость однокомнатных квартир в Москве [6].

Данные из газеты «Из рук в руки» за период с декабря 1996 г. по сентябрь 1997г.

Была выбрана Юго-Западная часть города, в которой высок спрос на жилые площади (всего 69 наблюдений). Файл example_01.xls.

 

Переменные:

N -                 Номер по порядку.

distc               Удаленность. от центра, км.

distm              Удаленность от метро, мин.

totsq               Общая площадь квартиры, кв.м.

kitsq               Площадь кухни, кв.м.

livsq               Площадь комнаты, кв.м.

floor               Этаж.  0-первый/последний, 1-нет.

cat                  Категория дома. 1-кирпичный, 0-нет.

price              Цена квартиры, тыс. USD.

 

Найдите среднее арифметическое, выборочное стандартное отклонение и другие статистики параметров. Найдите коэффициенты корреляции параметров с ценой квартиры. Соответствуют ли полученные значения экономической интуиции?

 

 

N	region	distc	distm	totsq	kitsq	livsq	floor	cat	price
1	Фрунзенская	4	10	34,00	7,50	19,00	1	1	54
2	Ленинский пр.	5,7	7	36,00	10,00	20,00	0	0	35
3	Ленинский пр.	5,7	12	45,00	13,00	20,00	1	1	59
4	Академическая	7,6	10	35,30	10,00	20,00	1	0	35
5	Университет	8,7	6	33,00	5,50	22,00	1	0	33
6	Нов.Черемуш.	10,3	3	33,00	8,50	18,00	1	1	57
7	Юго-Западная	13,3	10	37,00	10,00	19,00	1	0	43
8	Коньково	14,8	2	38,00	8,50	19,10	1	0	39
9	Фрунзенская	4	15	54,00	9,20	27,20	1	1	70
10	Университет	8,7	15	35,00	6,00	20,00	0	1	43
11	Пр.Вернадск.	11,4	10	31,40	5,20	21,30	1	0	33
12	Ленинский пр.	5,7	7	32,00	6,00	21,00	1	0	37
13	Нов.Черемуш	10,3	7	38,00	8,00	19,00	0	0	33
14	Университет	8,7	10	31,60	8,80	14,00	0	0	31
15	Юго-Запад	13,3	5	32,00	8,00	17,00	1	0	37
16	Юго-Запад	13,3	10	37,00	10,00	19,00	1	0	43
17	Ленинский пр.	5,7	5	32,00	8,00	17,00	1	1	38
18	Академическая	7,6	10	37,00	8,00	19,00	1	1	51
19	Академическая	7,6	15	32,20	6,50	17,00	0	1	30
20	Коньково	14,8	3	33,00	8,00	19,00	1	0	30
21	Коньково	14,8	5	37,50	9,60	19,80	1	0	36
22	Коньково	14,8	10	33,00	7,00	19,00	1	0	33
23	Университет	8,7	15	32,00	6,00	21,50	1	0	35
24	Пр.Вернадск.	11,4	5	29,70	6,00	16,10	0	0	28
25	Пр.Вернадск.	11,4	15	36,00	8,60	18,00	0	0	40
26	Юго-Запад	13,3	15	36,00	10,00	19,00	0	0	33
27	Ленинский пр.	5,7	2	31,60	6,00	21,60	1	1	35
28	Ленинский пр	5,7	5	52,00	12,00	34,00	1	1	75
N	region	distc	distm	totsq	kitsq	livsq	floor	cat	price
29	Коньково	14,8	3	36,00	10,00	19,00	1	0	40
30	Коньково	14,8	5	33,00	8,00	18,00	1	0	30
31	Университет	8,7	5	32,00	5,50	20,10	1	0	31
32	Академическая	7,6	15	35,00	9,80	20,00	1	0	37
33	Нов.Черемуш	10,3	15	38,00	10,00	19,50	1	0	40
34	Коньково	14,8	1	39,00	8,50	19,00	1	0	40
35	Фрунзенская	4	5	34,00	8,00	19,00	1	1	58
36	Фрунзенская	4	10	38,00	6,50	18,00	0	1	48
37	пр.Вернадск.	11,4	3	35,00	10,00	20,00	1	0	40
38	Юго-запад	13,3	7	36,00	9,00	19,50	1	0	42
39	Нов.Черемуш.	10,3	7	34,00	8,00	18,00	1	1	51
40	Коньково	14,8	5	38,00	8,50	19,00	1	0	43
41	Коньково	14,8	7	33,00	6,00	19,00	1	0	30
42	Коньково	14,8	10	32,00	8,00	17,00	1	0	40
43	Коньково	14,8	10	38,00	8,50	19,10	1	0	43
44	Академическая	7,6	5	43,00	8,50	25,00	0	1	53
45	Академическая	7,6	10	30,00	6,00	18,30	1	1	28
46	Коньково	14,8	7	34,80	7,80	17,80	0	0	29
47	Коньково	14,8	15	35,00	10,00	19,60	1	0	37
48	Коньково	14,8	3	32,80	6,50	18,50	1	0	30
49	НовЧеремуш.	10,3	10	39,00	9,00	19,00	1	0	45
50	Университет	8,7	15	49,00	9,00	20,50	0	1	52
51	Фрунзенская	4	3	32,00	6,20	19,00	1	1	53
52	Пр.Вернадск.	11,4	10	33,00	6,50	19,00	1	0	32
53	Пр.Вернадск.	11,4	15	32,30	6,00	21,90	0	0	28
54	Юго-Запад	13,3	10	30,00	7,00	19,80	1	0	34
55	Юго-Запад	13,3	10	34,00	9,00	19,00	1	0	42
56	Юго-Запад	13,3	7	33,00	7,00	19,00	0	0	33
57	Академическая	7,6	10	30,00	6,00	18,30	1	1	28
58	Академическая	7,6	15	32,00	6,00	18,00	1	0	30
59	Коньково	14,8	5	33,10	7,50	18,00	1	0	32
60	Коньково	14,8	2	38,00	7,50	19,00	1	0	41
61	Коньково	14,8	7	38,00	8,60	19,00	1	0	43
62	Коньково	14,8	5	37,30	6,50	19,00	1	0	31
63	Ленинский пр.	5,7	8	31,40	5,60	21,00	1	0	33
64	Ленинский пр.	5,7	7	52,00	10,00	34,00	1	1	60
65	Нов.Черемуш	10,3	15	30,00	6,00	17,00	1	1	37
66	Нов.Черемуш	10,3	5	36,00	11,00	20,00	1	0	41
67	Пр.Вернадск.	11,4	5	28,00	6,70	14,40	1	0	35
68	Пр.Вернадск.	11,4	10	31,40	5,20	21,30	1	0	33
69	Юго-Запад	13,3	5	32,00	8,00	17,00	1	0	37

 

В дальнейшем мы продолжим работу с этим файлом.

ВНИМАНИЕ!!! Все файлы, созданными Вами во время практического занятия, необходимо сохранять на личных дискетах (желательно в двух экземплярах на разных носителях).

Практическое занятие № 2.

«Применение Eviews при построении и анализе линейной однофакторной модели регрессии»

Пример 2. Имеются следующие данные по 10 фермерским хозяйствам области:

 

Необходимо:

1.     Создать файл с исходными данными в среде Excel (файл example_02.xls).

2.     Осуществить импорт исходных данных в Eviews.

3.     Создать workfile (рабочий файл).

4.     Найти значения описательных статистик по каждой переменной и объяснить их.

5.     Построить поле корреляции моделируемого (результативного) и факторного признаков. Объяснить полученные результаты.

6.     Найти значение линейного коэффициента корреляции и пояснить его смысл.

7.     Определить параметры уравнения парной регрессии и интерпретировать их. Объяснить смысл полученного уравнения регрессии.

8.     Оценить статистическую значимость коэффициента регрессии  и уравнения в целом. Сделать выводы.

9.     Объяснить полученное значение .

10. Построить эмпирическую и теоретическую линию регрессии и объяснить их.

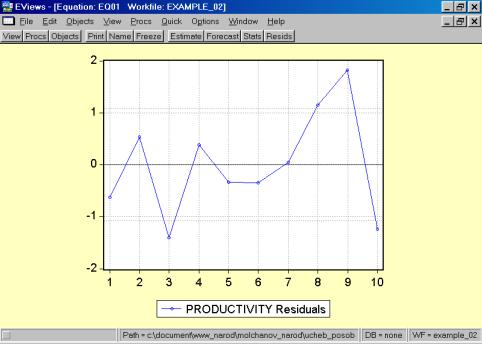
11. Построить и проанализировать график остатков.

12. С вероятностью 0,95 построить доверительный интервал для ожидаемого значения урожайности  по точечному значению .

13. Оформить отчет по занятию.

Порядок выполнения задания

1.     В Excel исходные данные должны быть организованы таким образом, чтобы в каждой колонке были представлены данные по соответствующей переменной (рис. 21). Имена переменных набираются латинскими буквами. Файл необходимо сохранить в формате Excel 5.0/95 (рис. 22). Введем обозначения: урожайность зерновых – переменная Productivity (зависимая, Y); внесено удобрений на  1 га посевов – Fertilizers (независимая, X).

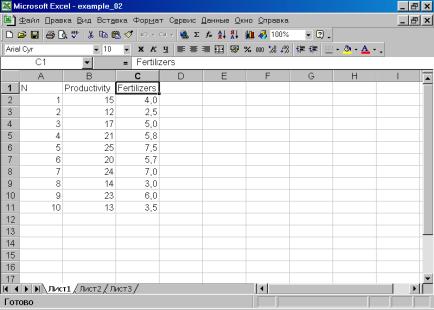
Рис. 21.

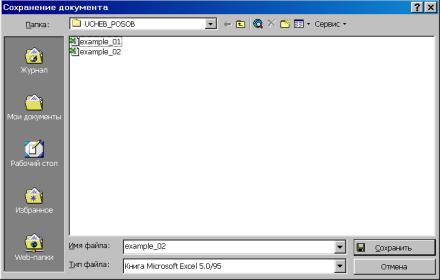
Рис. 22.

2.     Создаем рабочий файл для импортирования исходных данных из Excel в Eviews, работая с диалоговым окном File/New/Workfile (рис. 23), далее выбираем: Procs/Import/Read Text-Lotus-Excel (рис. 24).

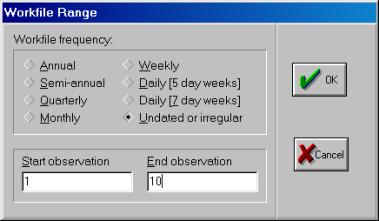
Рис. 23.

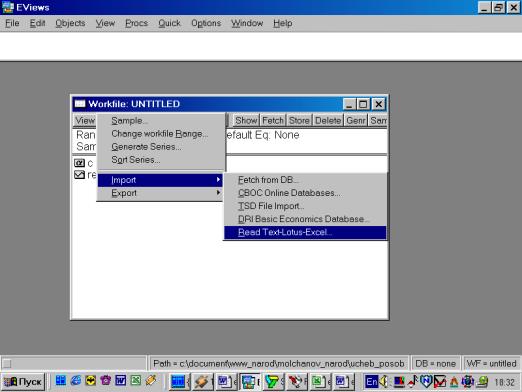
Рис. 24.

3.     Далее в открывшемся окне находим и выбираем файл Excel с исходными данными (файл не должен в этот момент использоваться любыми программами), осуществляя автоматический импорт исходных данных в workfile (рис. 25). В следующем открывшемся диалоговом окне нужно указать адрес ячейки, в которой записаны данные первого по счету наблюдения и число переменных  в рассматриваемом примере (рис. 26).. Если все выполнено правильно, то в открывшемся окне workfile должны появиться  имена переменных, а также константа (с) и остатки (resid) (рис. 27).

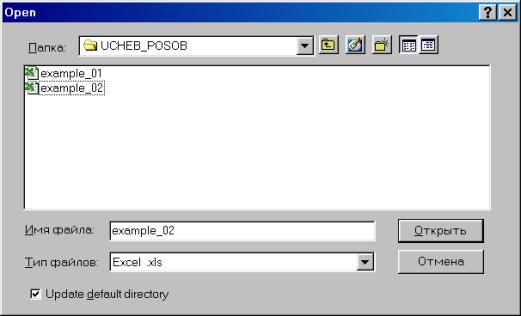
Рис. 25.

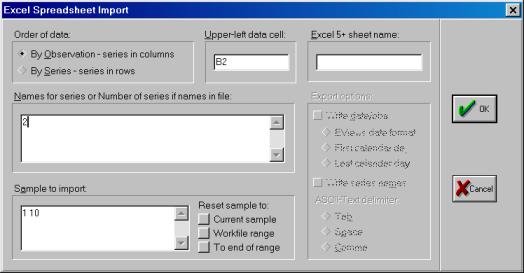
Рис. 26.

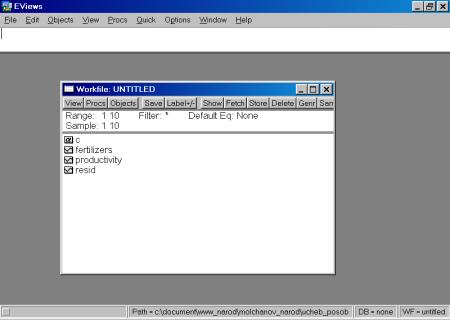
Рис. 27.

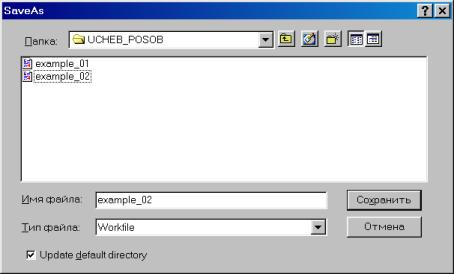
Рис. 28.

Сохраним рабочий файл (рис. 28).

4.     Значения описательных статистик находим следующим образом: в окне  workfile выделяем переменные, щелкаем мышкой по выделенной части и далее выбираем: Open/As Group/ (рис. 29). Открывается окно с исходными данными. Новую группу можно сохранить, выбрав опцию Name (рис. 30). Для просмотра описательных статистик View/Descriptive Stats/Common Sample (рис 31). Результат представлен на рис. 32.

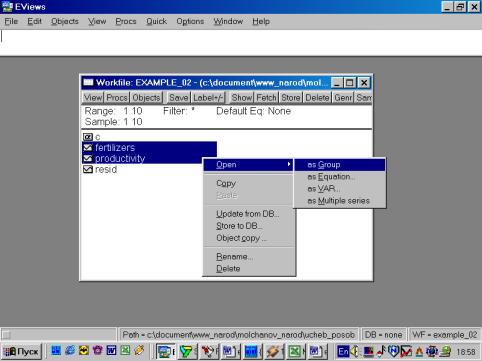
Рис. 29.

Рис. 30.

Рис. 31.

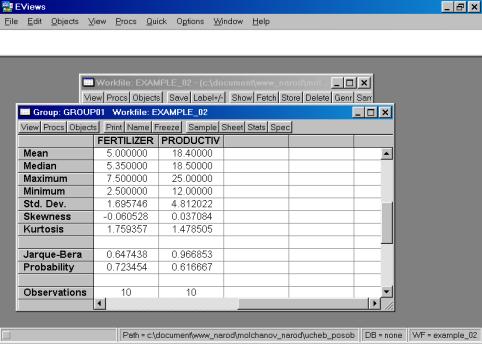
Рис. 32.

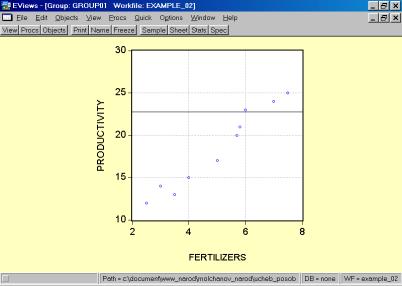
5.     В окне workfile (рис. 32) для построения поля корреляции необходимо выбрать следующие пункты меню: VIEW/GRAPH/SCATTER/SIMPLE SCATTER/ (рис. 33). Полученный в результате график представляет собой поле корреляции результативного и факторного признаков (рис. 34).

6.     В окне Workfile (используя созданную группу из двух переменных) выбрать:    /VIEW/CORRELATION/ (рис. 35). Полученная таблица - корреляционная матрица, в которой отражено значение коэффициента парной корреляции результативного и факторного признаков (рис. 36).

Рис. 33.

Рис. 34.

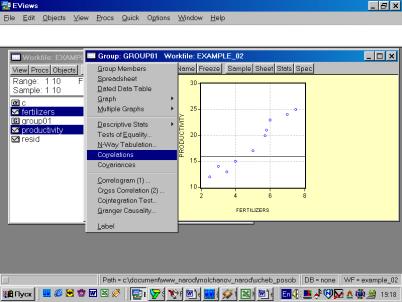
Рис. 35.

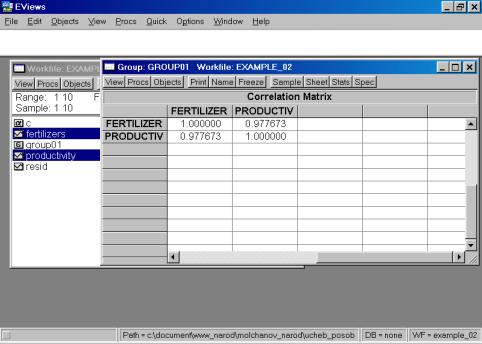
Рис. 36.

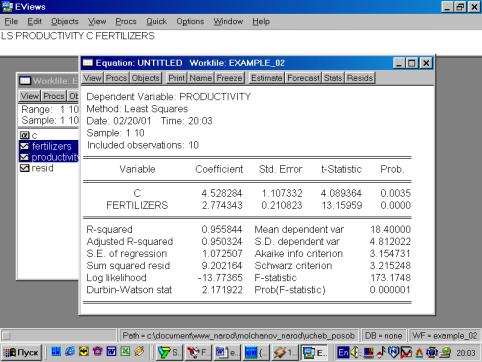
7.     В диалоговом окне описать в общем виде искомое уравнение: LS PRODUCTIVITY C FERTILIZERS <Enter> (метод наименьших квадратов (LS) эндогенная переменная, константа, экзогенная переменная), или выбрать в строке главного меню EVIEWS: QUICK/ESTIMATE EQUATION/ PRODUCTIVITY C FERTILIZERS (рис. 37). В открывшемся окне (рис. 38) должны быть переменные: зависимая переменная, применяемый метод, число наблюдений, параметры уравнения регрессии, стандартные  ошибки, значения t – статистик и соответствующие им вероятности, значение  и ряд других показателей.

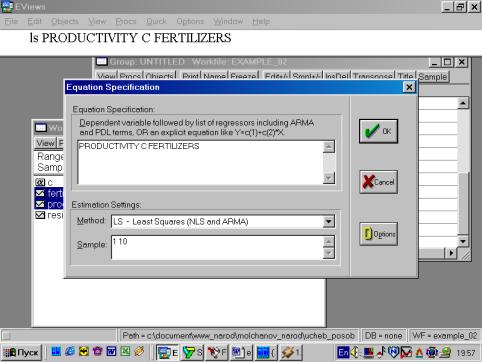
Рис. 37.

Рис. 38.

8. и 9. Результаты выполнения п.7 позволяют оценить статистическую значимость параметров уравнения регрессии и объяснить полученное значение R .

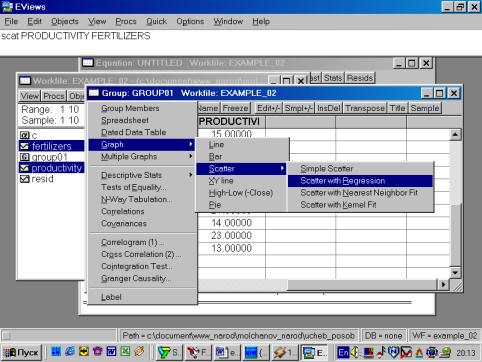
Рис. 39.

10. Для построения эмпирической линии регрессии в окне workfile выделить группу переменных и выбрать: VIEW/GRAPH/SCATTER/SCATTER WITH REGRESSION/ (рис. 39). В промежуточном окне (рис. 40) необходимо нажать <Ok>. Полученный график (рис. 41) – эмпирическая линия регрессии. Чтобы построить теоретическую (подогнанную) линию регрессии, необходимо найти теоретические (вычисленные с  помощью уравнения регрессии) значения результативного признака. Для этого открыть окно с параметрами уравнения регрессии, далее выбрать Forecast (рис. 42). Появится окно (рис. 43), в котором к исходным добавилась новая переменная PRODUCTIVIf (прогнозное, (теоретическое, выровненное) значение переменной PRODUCTIVITY).  Затем, выделив все переменные (включая теоретическое значение результативного признака), в командной строке записать SCAT FERTILIZERS PRODUCTIVITY PRODUCTIVIf. Полученный график (рис. 44) – теоретическая (подогнанная) линия регрессии.

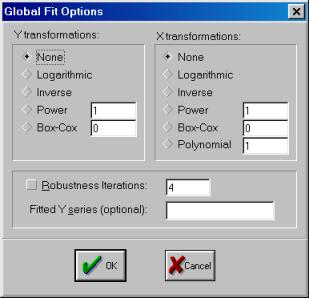
Рис. 40.

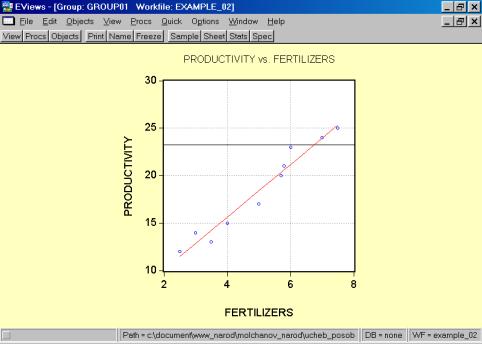
Рис. 41.

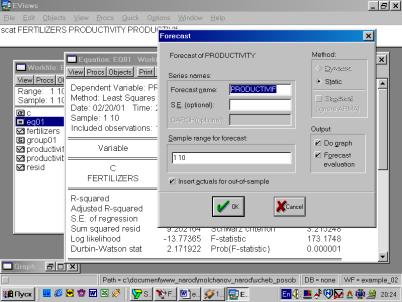
Рис. 42.

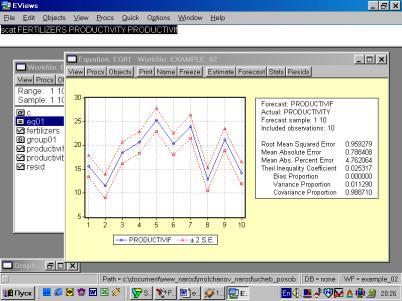
Рис. 43.

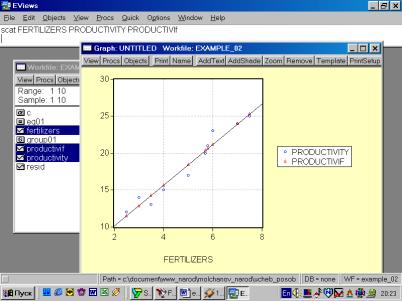
Рис. 44.

11. Данная операция возможна только в том случае, если ей предшествует построение регрессионного уравнения. В окне Workfile можно дважды щелкнуть на переменной Resid (рис. 45). Далее, выбрать: VIEW/LINE GRAPH/, или, открыв окно с параметрами уравнения регрессии, выбрать: VIEW /ACTUAL, FITTED…/ACTUAL, FITTED…TABLE/ (рис. 46). Результат представлен на рис. 47. Другой вариант вывода (фактические, предсказанные значения переменных, остатки, график остатков) – рис. 48.

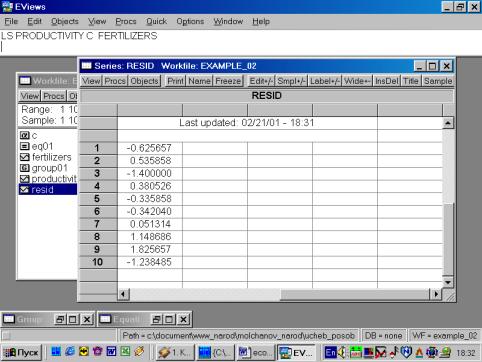
Рис. 45.

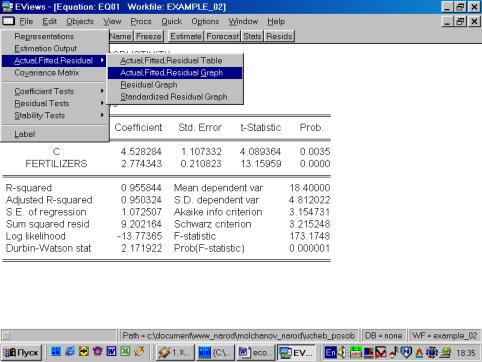
Рис. 46.

Рис. 47.

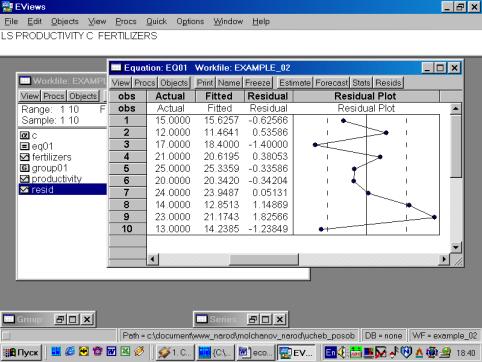
Рис. 48.

12. Для нахождения границ доверительного интервала в командной строке необходимо указать (рис. 49):

GENR XK = 5 * 1.05

GENR YFK = 4.53 +2.77*XK

GENR h = ((1 + 0.25^2)/1.6957^2) ^0.5

GENR CI = 2.31*(1.07/10^0.5)*h

В результате искомые границы определяются следующим образом:

YFKCI , т.е. от YFK+CI до YFK-CI (см. рис. 50).

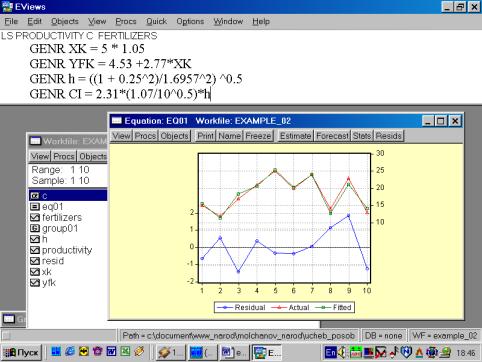
Рис. 49.

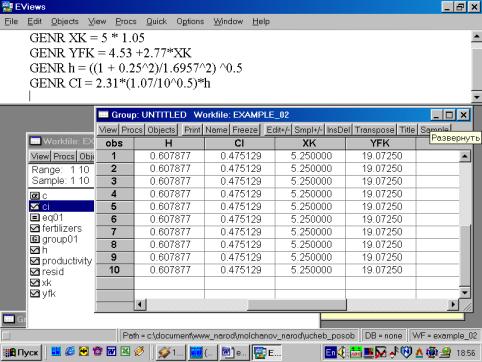
Рис. 50.

13. Оформить отчет по занятию.

Отчет должен содержать: подробные пояснения расчетов, ссылки на используемые формулы, результаты работы Eviews в виде экранных копий, другую, необходимую на Ваш взгляд, информацию.

Практическое занятие № 3.

«Применение Eviews при построении и анализе линейной однофакторной модели регрессии»

Выполняется самостоятельно.

Пример 3. Компания American Express Company в течение долгого времени полагала, что владельцы ее кредитных карточек имеют тенденцию  путешествовать более интенсивно, как по делам бизнеса, так и для развлечений. Как часть объемного исследования, проведенного Нью-Йоркской компанией рыночных исследований по заказу American Express Company, было осуществлено определение взаимосвязи между путешествиями и расходами владельцев кредитных карточек. Исследовательская фирма случайным образом выбрала 25 владельцев карточек из компьютерного файла American Express Company и записала суммы их общих расходов за определенный период времени. Для выбранных владельцев карточек фирма так же подготовила и разослала по почте вопросы о числе миль, которые провел в путешествиях владелец карточки за изучаемый период. Данные, полученные из опроса, составляют исходную информацию анализа (Х – число миль, проведенных в пути; У – расходы путешественников (усл. ден ед.)[1].

1.     Создать файл с исходными данными в среде Excel (файл example_03.xls).

2.     Осуществить импорт исходных данных в Eviews.

3.     Создать рабочий файл (workfile).

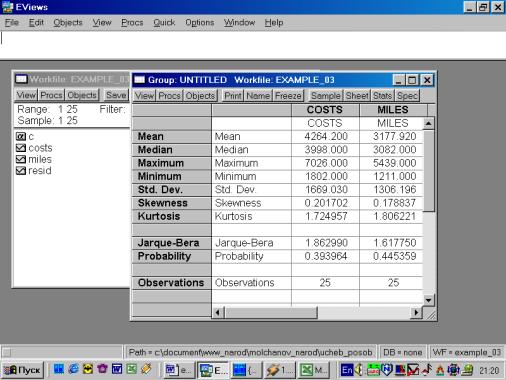
4.     Найти значения описательных статистик по каждой переменной и объяснить их (рис. 51).

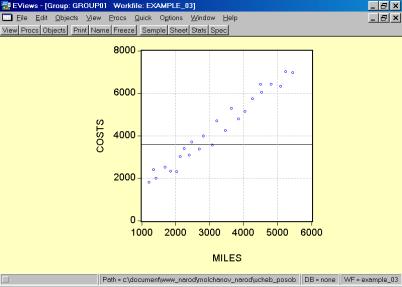
5.     Построить поле корреляции моделируемого (результативного) и факторного признаков (рис. 52). Объяснить полученные результаты.

6.     Найти значение линейного коэффициента корреляции и пояснить его смысл (рис. 53).

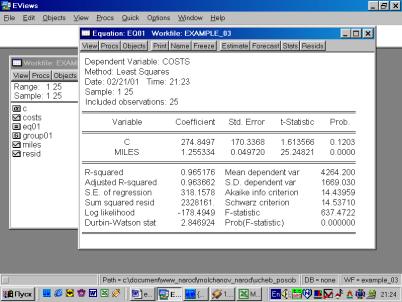
7.     Определить параметры уравнения парной регрессии и интерпретировать их. Объяснить смысл полученного уравнения регрессии (рис. 54).

8.     Оценить статистическую значимость коэффициента регрессии  и уравнения в целом. Сделать выводы.

9.     Объяснить полученное значение .

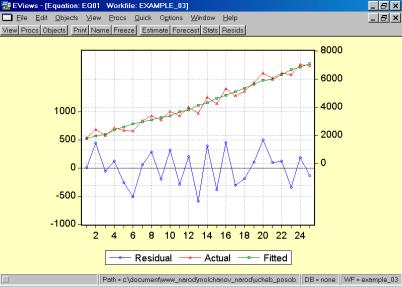
10. Построить эмпирическую и теоретическую линию регрессии и объяснить их (рис. 55).

11. Построить и проанализировать график остатков (рис. 56).

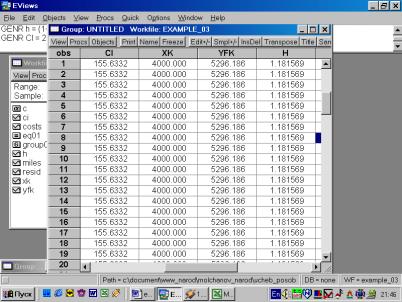
12. С вероятностью 0,95 построить доверительный интервал для оценки ожидаемого значения средних расходов владельцев карточек, дальность путешествий которых составила 4000 миль (рис. 57).

13. Оформить отчет по занятию.

Результаты расчетов:

Рис. 51.

Рис. 52.

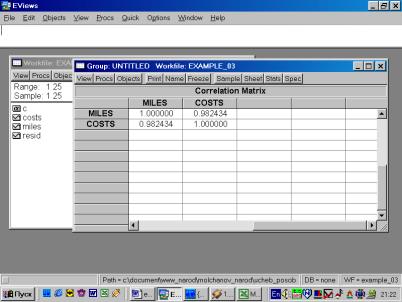
Рис. 53.

Рис. 54.

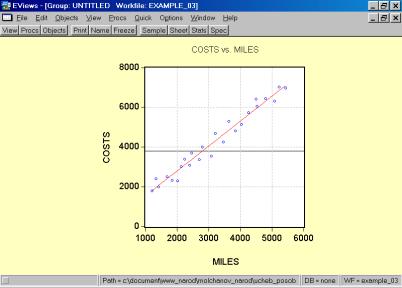
Рис. 55.

Рис. 56.

Рис. 57.

Практическое занятие № 4.

«Применение Eviews при построении и анализе многофакторной модели регрессии. Выявление мультиколлинеарности и гетероскедастичности в модели. Проверка спецификации модели»

Пример 4. Имеются данные о вариации дохода  кредитных организаций США за период 25 лет в зависимости от изменений годовой ставки по сберегательным депозитам и числа кредитных учреждений[2].

Введем следующие обозначения:

    – прибыль кредитных организаций, %;

 - чистый доход на 1$ депозита;

– число кредитных учреждений.

1.     Создать файл с исходными данными в среде Excel (файл example_04.xls).

2.     Осуществить импорт исходных данных в Eviews.

3.     Создать workfile.

4.     Найти значения описательных статистик по каждой переменной и объяснить их (рис. 58).

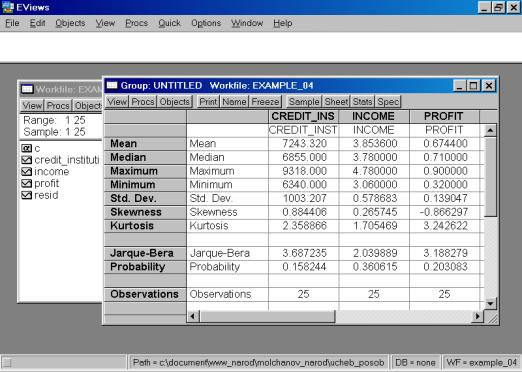
Рис. 58.

5.     Построить корреляционную матрицу для всех переменных, включенных в модель (рис. 59).

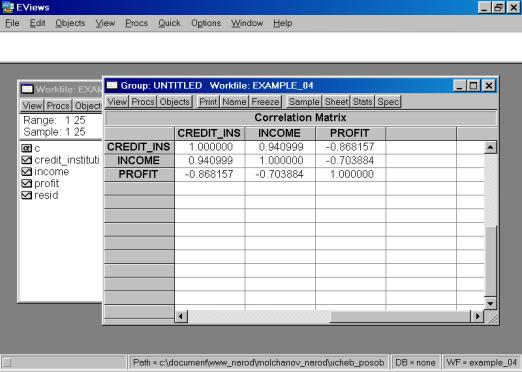
Рис. 59.

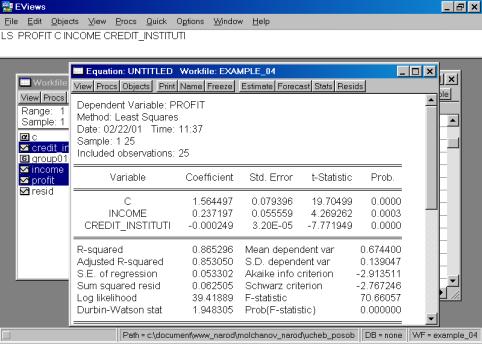
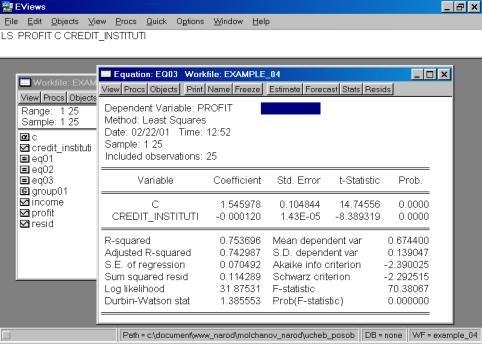
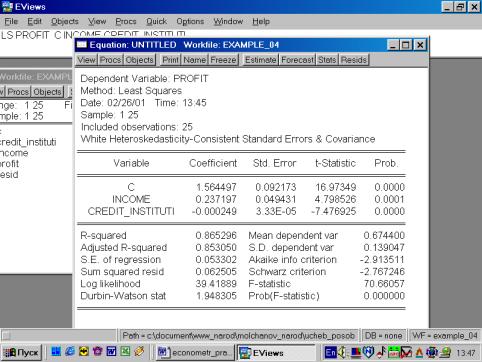
6.     Построить регрессионное уравнение МНК, в котором зависимая переменная – прибыль кредитных организаций, а независимые – чистый доход на 1$ депозита и число кредитных учреждений (рис. 60, 61).

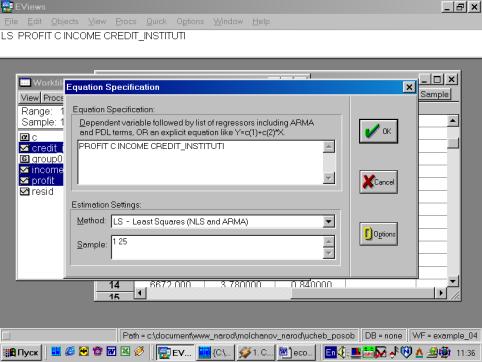
Рис. 60.

Рис. 61.

Уравнение примет следующий вид:

.

Подставим полученные оценки из итоговой формы вывода:

.

7.     Оценить статистическую значимость параметров полученного уравнения и всей модели в целом.

8.     Проверить наличие мультиколлинеарности в модели. Сделать вывод.

Мультиколлинеарность – это коррелированность двух или нескольких объясняющих переменных  в уравнении регрессии. В результате высококоррелированные объясняющие переменные действуют в одном направлении и имеют недостаточно независимое колебание, чтобы дать возможность модели изолировать влияние каждой переменной. Проблема мультиколлинеарности возникает только в случае множественной регрессии. Мультиколлинеарность особенно часто имеет место при анализе макроэкономических данных (например, доходы, производство). Получаемые оценки оказываются нестабильными как в отношении статистической значимости, так и по величине и знаку (например, коэффициенты корреляции). Следовательно, они ненадежны. Значения  коэффициентов R² могут быть высокими, но стандартные ошибки тоже высоки, и отсюда  t- критерии малы, отражая недостаток значимости.

Для проверки появления мультиколлинеарности  применяются два метода, доступные во всех статистических пакетах[3]:

Ø     Вычисление матрицы коэффициентов корреляции для всех объясняющих переменных. Если коэффициенты корреляции между отдельными объясняющими переменными  очень велики, то, следовательно, они коллинеарны. Однако, при этом не существует единого правила, в соответствии с которым есть некоторое пороговое значение коэффициента корреляции, после которого высокая корреляция может вызвать отрицательный эффект и повлиять на качество регрессии.

Ø     Для измерения эффекта мультиколлинеарности используется показатель VIF – «фактор инфляции вариации»:

ü 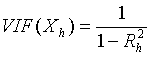        , где    - значение коэффициента множественной корреляции, полученное для регрессора  как зависимой переменной и остальных переменных . При этом степень мультиколлинеарности, представляемая в регрессии переменной , когда переменные  включены в регрессию, есть функция множественной корреляции между  и другими переменными .

ü     Если , то объясняющие переменные, коррелирующие между собой,  считаются мультиколлинеарными.

Существует еще ряд способов, позволяющих обнаружить эффект мультиколлинеарности:

Ø     Стандартная ошибка регрессионных коэффициентов близка к нулю.

Ø     Мощность коэффициента регрессии отличается от ожидаемого значения.

Ø     Знаки коэффициентов регрессии противоположны ожидаемым.

Ø     Добавление или удаление наблюдений из модели сильно изменяют значения оценок.

Ø     Значение F-критерия существенно, а t-критерия – нет.

Для устранения мультиколлинеарности может быть принято несколько мер:

Ø     Увеличивают объем выборки по принципу, что больше дан­ных означает меньшие дисперсии оценок МНК. Проблема реализации этого варианта решения состоит в трудности на­хождения дополнительных данных.

Ø     Исключают те переменные, которые высококоррелированны с остальными. Проблема здесь заключается в том, что воз­можно переменные были включены на теоретической основе, и будет неправомочным их исключение только лишь для то­го, чтобы сделать статистические результаты «лучше».

Ø     Объединяют данные кросс-секций и временных рядов. При этом методе берут коэффициент из, скажем, кросс-секционной регрессии и заменяют его на коэффициент из эквивалентных данных временного ряда.

Проделанные манипуляции позволяют предположить, что мультиколлинеарность может присутствовать (оценки  любой регрессии будут страдать от нее в определенной степени, если только все независимые переменные не окажутся абсолютно некоррелированными), однако в данном примере это не влияет на результаты оценки регрессии. Следовательно, выделять «лишние» переменные не стоит, так как это отражается на содержательном смысле модели.

9.     Проверить спецификацию модели. Объяснить полученные результаты.

Подробно теоретические вопросы, связанные с проблемами спецификации эконометрических моделей, были рассмотрены в лекционном курсе.

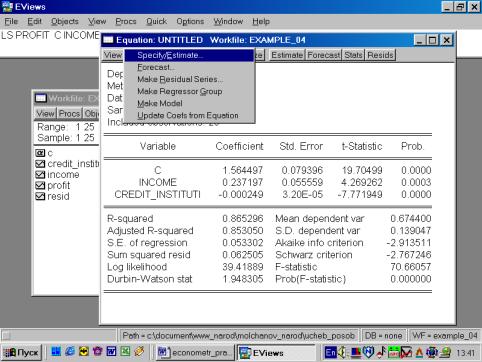
В нашем случае мы ограничимся тем, что попробуем исключить поочередно независимые переменные. Первой исключаем переменную CREDIT_INSTITUTI (рис. 62). Коэффициент при переменной INCOME изменил знак на противоположный.

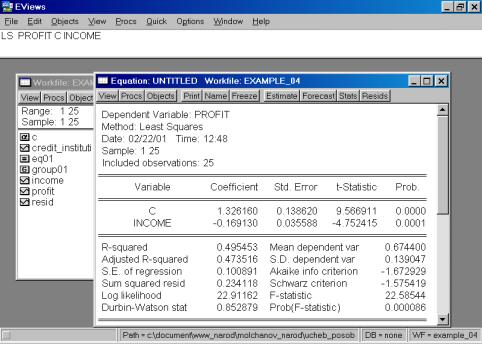
Рис. 62.

Рис. 63.

В случае исключения из первоначальной модели переменной INCOME, знак регрессионного коэффициента при переменой CREDIT_INSTITUTI остался без изменения (рис. 63). Представляется разумным разделять эффект двух независимых переменных на зависимую переменную в модели с совместным их влиянием в регрессионном уравнении. Данный пример иллюстрирует важность использования множественной регрессии вместо парной в случае, когда изучаемое явление существенно детерминирует несколько независимых переменных.

10. Проверить наличие гетероскедастичности в модели. Объяснить полученные результаты.

Если остатки имеют постоянную дисперсию, они называются гомоскедастичными, но если они непостоянны, то гетероскедастичными. Гетероскедастичность приводит к тому, что коэффи­циенты регрессии больше не представляют собой лучшие оценки или не являются оценками с минимальной дисперсией, следова­тельно, они больше не являются наиболее эффективными коэф­фициентами.

Воздействие гетероскедастичности на оценку интервала прогнозирования и проверку гипотезы заключается в том, что хотя коэффициенты не смещены, дисперсии и, следовательно, стандартные ошибки этих коэффициентов будут смещены. Если смещение отрицательно, то оценочные стандартные ошибки бу­дут меньше, чем они должны быть, а критерий проверки будет больше, чем в реальности. Таким образом, мы можем сделать вывод, что коэффициент значим, когда он таковым не является. И наоборот, если смещение положительно, то оценочные ошиб­ки будут больше, чем они должны быть, а критерии проверки – меньше. Значит, мы можем принять нулевую гипотезу, в то вре­мя как она должна быть отвергнута.

Проверкой на гетероскедастичность служит тест Голдфелда-Кванта. Он требует, чтобы остатки были разделены на две груп­пы из  наблюдений, одна группа с низкими, а другая – с высо­кими значениями. Обычно срединная одна шестая часть наблю­дений удаляется после ранжирования в возрастающем порядке, чтобы улучшить разграничение между двумя группами. Отсюда число остатков в каждой группе составляет , где  пред­ставляет одну шестую часть наблюдений.

Критерий Голдфелда-Кванта – это отношение суммы квадра­тов отклонений (СКО) высоких остатков к СКО низких остатков:

.

Этот критерий имеет распределение с  степе­нями свободы.

Чтобы решить проблему гетероскедастичности, нужно иссле­довать взаимосвязь между значениями ошибки и переменными и трансформировать регрессионную модель так, чтобы она отра­жала эту взаимосвязь. Это может быть достигнуто посредством регрессии значений ошибок по различным формам функций пе­ременной, которая приводит к гетероскедастичности, например,

,

где - независимая переменная (или какая-либо функция не­зависимой переменной), которая предположительно является причиной гетероскедастичности, а  отражает степень взаимо­связи между ошибками и данной переменной, например,  или  и т. д.

Следовательно, дисперсия коэффициентов запишется:

.

Отсюда если , мы трансформируем регрессионную мо­дель к виду:

.

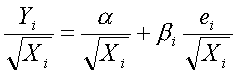Если , т.е. дисперсия увеличивается в пропорции к квадрату рассматриваемой переменной , трансформация при­обретает вид:

.

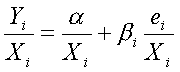Используя Eviews, можно провести проверку и устранение гетероскедастичности следующим образом:

Ø     Запустить стандартную регрессию.

Ø     Вычислить остатки.

Ø     Запустить регрессию с использованием квадрата остатков как зависимой переменной и оценить зависимую переменную  как независимую переменную (тест White).

Ø     Оценить nR², где n – объем выборки, R² – коэффициент детерминации.

Ø     Использовать статистику с одной степенью свободы (в EVIEWS – используется F – статистика) для проверки существенности отличия  nR² от нуля.

Ø     Основным способом устранения гетероскедастичности является применение взвешенного метода наименьших квадратов.

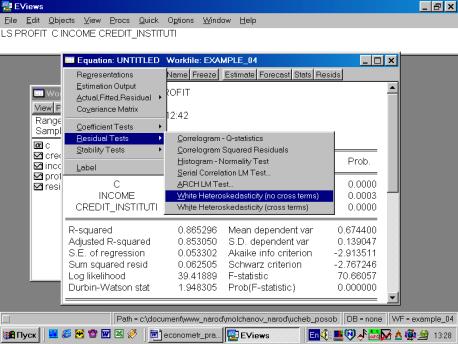
Выбираем тест White (см. рис. 64).

Рис. 64.

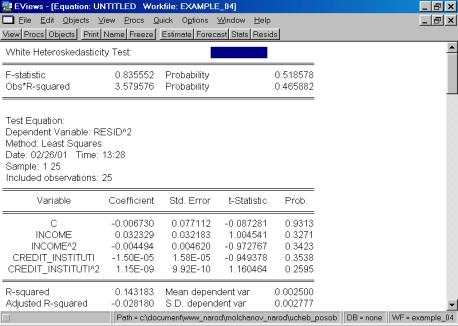
Итог формы вывода представлен на рис. 65.

Рис. 65.

Как следует из приведенной распечатки, вероятность ошибки первого рода равна 51,86%. Следовательно, нулевую гипотезу (об отсутствии гетероскедастичности) нельзя отклонить.

Для случая, когда гетероскедастичность присутствует, проблему гетероскедастичности можно решать следующим образом:

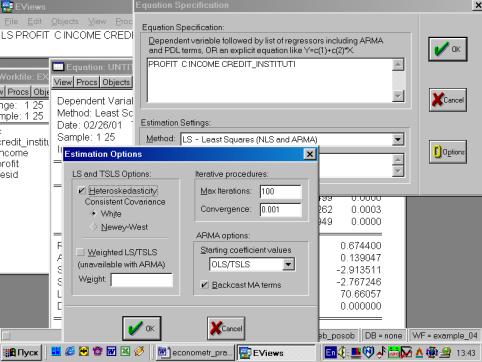
Выбираем в пунктах меню текущего окна опцию Proc/Specify/Estimate… (рис. 66). Появляется окно оценки регрессии, где необходимо нажать клавишу Options и в появившимся окне отметить Heteroskedasticity  (рис. 67).

Рис. 66.

Рис. 67.

Появилось новое, переоцененное уравнение (рис. 68). Полученное уравнение можно вновь проверить по тесту White.

Рис. 68.

11. Оформить отчет.

 

 

 

 

 

Практическое занятие № 5.

«Фиктивные переменные»

Иногда необходимо включение в регрессионную модель одной или более качественных переменных (например, разделение по полу: мужской и женский; по уровню образования: общее и профессиональное и т.д.). Альтернативно может понадобиться сде­лать качественное различие между наблюдениями одних и тех же данных. Так, если проверяется взаимосвязь между разме­ром компании и месячными доходами по акциям, может быть желательным включение качественной переменной, представ­ляющей месяц январь, по причине хорошо известного «январского эффекта» во временных рядах доходов по ценным бумагам. Данный «январский эффект» - это феномен, за­ключающийся в том, что средние доходы по акциям, особенно небольших компаний, в среднем выше в январе, чем в другие месяцы. Таким образом, если мы рассматриваем январские на­блюдения как качественно отличные от других наблюдений, фиктивная переменная  позволит произвести подобное качественное различие.

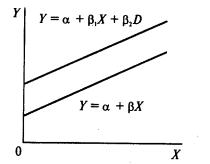
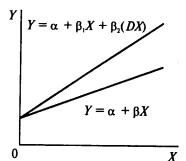
Фиктивные переменные бывают двух типов - сдвига и на­клона. Фиктивная переменная сдвига - это переменная, которая меняет точку пересечения линии регрессии с осью ординат в случае применения качественной переменной (рис. 69). Фиктивная пере­менная наклона - это та переменная, которая изменяет наклон линии регрессии в случае использования качественной перемен­ной (рис. 70). Оба типа фиктивных переменных будут иметь значение  или , когда наблюдения данных совпадают с уместной ко­личественной переменной, но будут иметь нулевое значение при совпадении с наблюдениями, где эта качественная переменная отсутствует.

Пример 5. По данным примера  1 (файл example_01.xls.) дать интерпретацию бинарным, «фиктивным» переменным, принимающим значения 0 или 1: floor – принимает значение 0, если квартира расположена на первом или последнем этаже,  cat –принимает значение 1, если квартира находится в кирпичном доме.

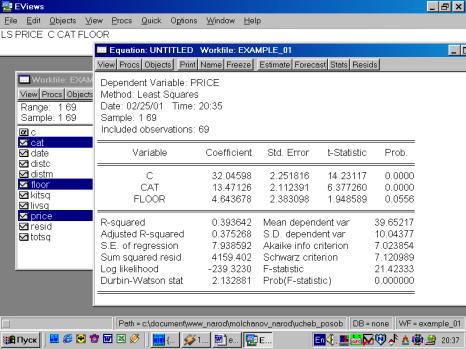
Построим регрессионное уравнение вида LS PRICE C CAT FLOOR (рис 71). Тем самым мы предполагаем (хотя в действительности это может быть и не так), что на цену квартиры оказывают влияние только две, указанные выше, составляющие. В результате получится уравнение следующего вида (рис 72):

.

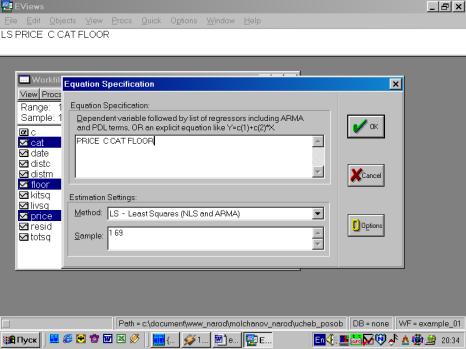
Рис. 71.

Рис. 72.

Используя результаты оценивания уравнения, содержащиеся в форме вывода (рис. 72), можно записать такое уравнение:

.

Как же можно интерпретировать полученные результаты? Полученный коэффициент при CAT означает, что квартиры в кирпичных домах стоят в среднем на $13471 дороже аналогичных квартир в панельных домах. Коэффициент при FLOOR может быть интерпретирован так: квартиры на не первом/последнем этажах стоят в среднем на $4644 дороже аналогичных, расположенных на первом/последнем этажах.

 

 

СОДЕРЖАНИЕ
1.	Предисловие	3
2.	Практическое занятие № 1. «Знакомство с эконометрическим пакетом Eviews»	4
3.	Практическое занятие № 2.  «Применение Eviews при построении и анализе линейной однофакторной модели регрессии»	18
4.	Практическое занятие № 3. «Применение Eviews при построении и анализе линейной однофакторной модели регрессии»	32
5.	Практическое занятие № 4. «Применение Eviews при построении и анализе многофакторной модели регрессии. Выявление мультиколлинеарности и гетероскедастичности в модели. Проверка спецификации модели»	36
6.	Практическое занятие № 5. «Фиктивные переменные»	46
7.	Практическое занятие № 6. «Однофакторные стохастические модели динамических процессов»	48

 

КОМПЬЮТЕРНЫЙ ПРАКТИКУМ ПО НАЧАЛЬНОМУ КУРСУ ЭКОНОМЕТРИКИ (РЕАЛИЗАЦИЯ НА EVIEWS)

 

 

 

Практикум

 

 

 

 

Молчанов Игорь Николаевич

Герасимова Ирина Алексеевна

 

 

 

 

 

 

 

 

 

 

 

Ответственная за выпуск

Начальник РИО РГЭУ В.Е. Смейле

Редактирование и корректура авторов

Оригинал-макет И.Н.Молчанов

 

 

 

 

 

 

 

Лицензия ЛР N 020276 от 18.02.97

Государственного Комитета Российской Федерации по печати

 

344007, Ростов-на-Дону, ул. Большая Садовая, 69, РГЭУ «РИНХ», Издательство

Отпечатано в копировально-множительном центре.

Ростов-на-Дону, ул. Большая Садовая, 79. ПБОЮЛ Зайчиков О.Б.